الصفحة الرئيسية نظرية ثفنن مختبر كهرباء حساب مقسم جهد

حاسبة لحل اسئلة التحليل الشبكي مع إمثلة توضيحية

موسوعة المهندس الكهربائي
Dev : Taher

قاعدة كرامر ’ ؛ آلة حاسبة لتحليل الدارات الخطية | خطوة بخطوة مع الأمثلة المحلولة

اليوم ، سوف نشارك طريقة أخرى بسيطة لكنها قوية تقنية تحليل الدوائر وهو ما يعرف ب “ قاعدة كرامر “.


يوجد أدناه البرنامج التعليمي خطوة بخطوة للأمثلة التي تم حلها ، والتي توضح كيفية حل دائرة كهربائية معقدة وشبكة بواسطة قاعدة كرامر.

Cramer’s Rule Calculator for 2×2 (نظام معادلتين)

: Cramer’s Rule Calculator 2 x 2 (حاسبة قاعدة كرامر نظام المعادلتين)
I 1+ I 2=
I 1+ I 2=
I 1 =
I 2 =

إيجاد متغيرين بواسطة قاعدة كرامر:

مثال 1 :

(في هذه الحالة ، فإن القيم المجهولة هي تياران i 1 و i 2 ) بواسطة قاعدة كرامر. لنبدأ الآن :

كما هو موضح أدناه ، هذه دائرة كهربائية بسيطة وسوف نقوم بحلها بواسطة قاعدة كرامر.

Cramer's rule. step by step procedure with solved example
.قاعدة كرامر لتحليل الدائرة الخطية | 2 متغير (2 × 2) مثال محلول

الحل :

الان نقوم بجمع قيم المقاومات المربوطة على التوالي (Ω 5)فيصبح مجموع(Ω 10)

قم بتطبيق تحليل الشبكة والتبسيط بواسطة قاعدة كرامر للعثور على القيم المجهولة للتيارات i 1و i 2.

الان , سنطبق (KVL) للتيارات المجهولة :

وبتطبيق قانون كيرشوف للفولطيات (KVL) على لوب 1 :

6 = 14 i 1+ 10( i 1– i 2)
6 = 24 i 1– 10 i 2….. → Eq (1)

وايظاً , بتطبيق قانون كيرشوف (KVL) للفولطيات في لوب 2 :

-5 = 10 i 2+ 10( i 2– i 1)
-5 = – 10 i 1+ 20 i 2….. → Eq (2)

هنا حصلنا على معادلتين ، أي

24 i 1 – 10 i 2 = 6
– 10 i 1 + 20 i 2 = -5

الآن ، سنحل هاتين المعادلتين بقاعدة كرامر لإيجاد القيم المجهولة (للتيارات) ، وهي


i 2 و i 1

الحل بقاعدة كرامر:

الخطوة 1:

أولاً ، اكتب المعادلات أعلاه في شكل مصفوفة. أي

الخطوة 2:

الآن ، اكتب مصفوفة المعامل للمعادلات أعلاه واسمها ∆. تأكد من أنه مربع ، أي عدد الصفوف × عدد الأعمدة. في الحالة أعلاه ، تتكون من صفين وعمودين.

الخطوة 3:

الآن أوجد المحدد | ∆ | لمصفوفة المعامل ∆ بالطريقة التالية. (سيساعدك الشكل أدناه على القيام بذلك).

Cramer's rule. step by step procedure with solved examples of two and three variables
إيجاد مصفوفة المعامل ∆ لقاعدة كرامر. شرح سهل

حسب الشكل أعلاه. ستكون الخطوة الأخيرة على هذا النحو

Cramer's rule. easiest method ever to solve equations

الخطوة 4:

الآن أوجد معامل المعامل المحدد Δ1 بنفس الطريقة المذكورة أعلاه ، ولكن استبدل العمود الأول من Δباستخدام "عمود الإجابة" (إذا لم تحصل على نقطة عمود الإجابة ، فراجع الشكل في الخطوة 2 أعلاه أو تحقق من الرسوم البيانية في نهاية المثال ، وقم فقط بالرجوع إلى المثال الثاني أدناه ، حيث قمنا بعمل نفس الشيء لتجد Δ1 )

cramer's rule

الخطوة 5:

الآن أوجد معامل المعامل المحدد Δ2 ، فقط استبدل العمود الثاني بـ "عمود الإجابة" وهو

cramer's rule. easy explanation.png

الخطوة 6:

كما تنص قاعدة كرامر على ذلك

{ i 2 = Δ 2 / Δ و i 1 = Δ 1 / Δ }

الآن ، ابحث i 1و i 2 بواسطة قاعدة كرامر

cramer's rule 2x2
i 1 = 0.184.2 A or 184.2 mA

و أيظاً ,

cramer's rule formula

i 2 = 0.157.9 A or 157.9 mA

أدناه هو ملخص رسوم بيانية لقاعدة كرامر لتحديد اثنين من المتغيرات أو القيم غير المعروفة

Cramer's Rule Simple Steps Infographics Chart
مخطط Infographics للخطوات البسيطة للقاعدة من كريمر

حسنًا ، كان الأمر سهلاً ... الآن ، ماذا عن 3 متغيرات…. لنحاول حل 3 متغيرات معادلات خطية بمساعدة قاعدة كرامر.

إيجاد ثلاثة متغيرات من خلال قاعدة كرامر:

(في هذه الحالة ، هذه القيم المجهولة هي ثلاث تيارات i 1 , i 2 و i 3 ) بواسطة قاعدة كرامر. الآن ، لنبدأ.

حاسبة قاعدة كرامر لـ 3 × 3 (نظام المعادلات الثلاث)

حاسبة قاعدة كرامر لـ 3 × 3 (نظام المعادلات الثلاث)
I 1+ I 2+ I 3=
I 1+ I 2+ I 3=
I 1+ I 2+ I 3=
I 1=
I 2=
I 3=

مثال 2 :

استخدم تحليل الشبكة لتحديد التيارات الشبكية الثلاثة في الدائرة أدناه. استخدم قاعدة كريمر للتبسيط

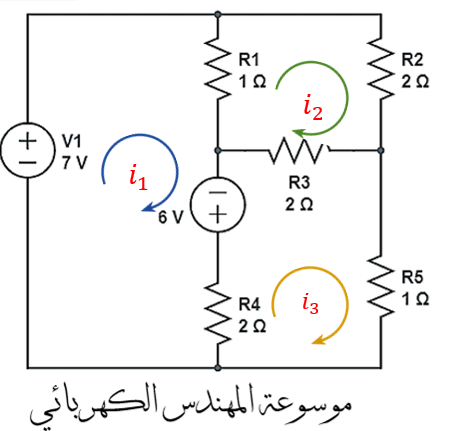
.ابحث عن القيم الثلاثة غير المعروفة للتيارات بواسطة قاعدة كرامر

الحل :

وبتطبيق قانون كيرشوف للفولطيات (KVL) في لوب رقم 1

-7+1( i 1– i 2) +6+2( i 1– i 3) = 0
1( i 2– i 1) + 2 i 2+ 3( i 2– i 3) = 0
2( i 3– i 1) – 6+3( i 3– i 2) +1 i 3= 0

دعونا نبسط المعادلتين لتصبح,

3 i 1– i 2– 2 i 3= 1 … Eq….. (1)
– i 1+ 6 i 2– 3 i 3= 0 … Eq….. (2)
-2 i 1– 3 i 2+ 6 i 3= 6 … Eq….. (3)

الآن ، اكتب المعادلات أعلاه في صورة المصفوفة.

3 i 1– i 2– 2 i 3= 1
– i 1+ 6 i 2– 3 i 3= 0
-2 i 1– 3 i 2+ 6 i 3= 6
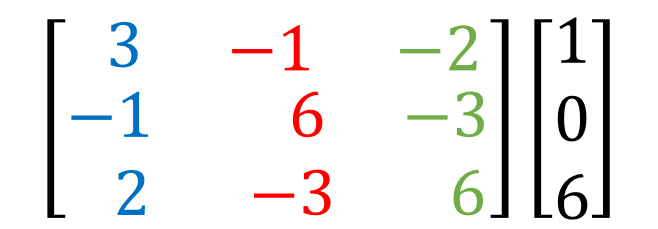
solving three equations sytem by cramer's rule

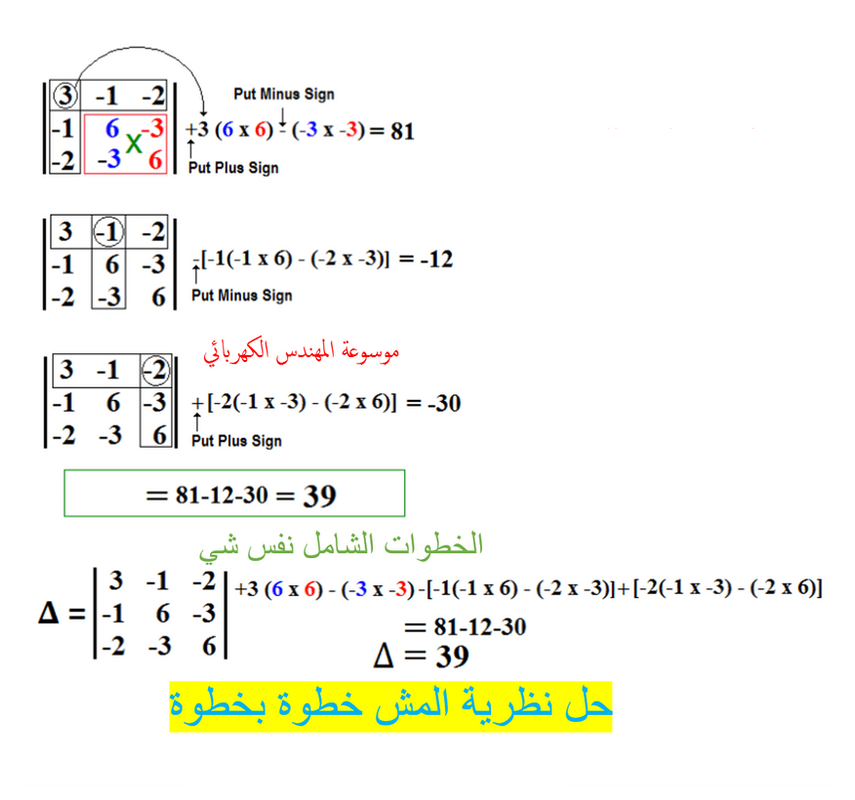
الآن ، سنجد محدد معامل ∆. كيف سنقوم بذلك؟ ما عليك سوى التحقق من الشكل أدناه للحصول على شرح أفضل.

وبشكل الاتي :

∆ = 81 -12 -30 = 39

الآن ، ابحث عن 1∆ بنفس الطريقة الموضحة أعلاه. ولكن ، فقط استبدل العمود الأول من المصفوفة بـ "عمود الإجابة". لمزيد من التفاصيل ، تحقق من الشكل الموضح أدناه.

cramer's rule. easy explanation
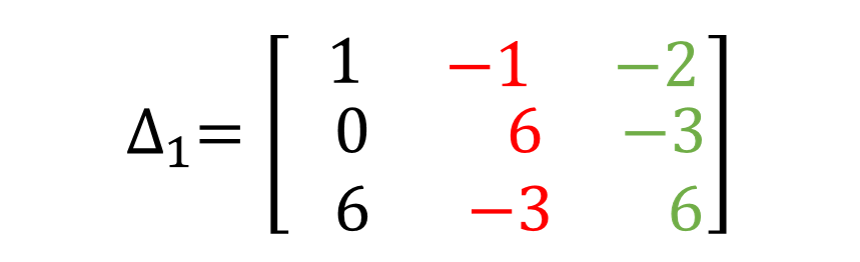
إذن ، هذه هي الخطوة الكاملة للعثور على 1∆ . هنا ، قمنا باستبدال "Blue Guys" في العمود الأول بـ "Black Guys" :). solving electric circuits by cramer rule
∆ 1= + 1(36-9) – ( –1 [0+18]) – 2(0-36)
∆ 1= 27 + 18 + 72
∆ 1= 117

مرة أخرى ، ابحث عن 2∆ بنفس الطريقة الموضحة سابقًا. فقط استبدل العمود الثاني من المصفوفة بـ "عمود الإجابة" ، أي استبدل "Red guys" في العمود الأوسط بـ "Black Guys" كما هو موضح أدناه.

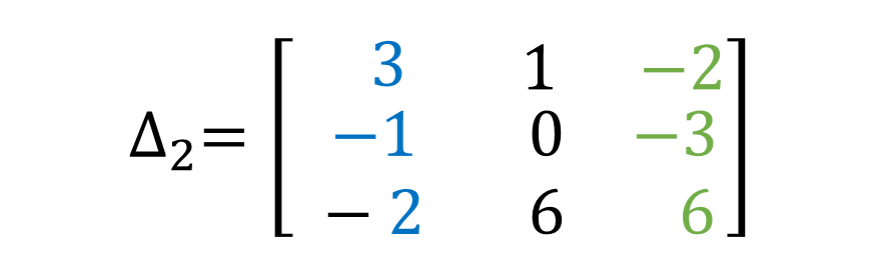
solve linear circuits by cramer's rule
∆ 2= + 3(0 +18) -1[(-6)-(+6)] – 2(-6-0)
∆ 2= 54+12+12 = 78
∆ 2= 78
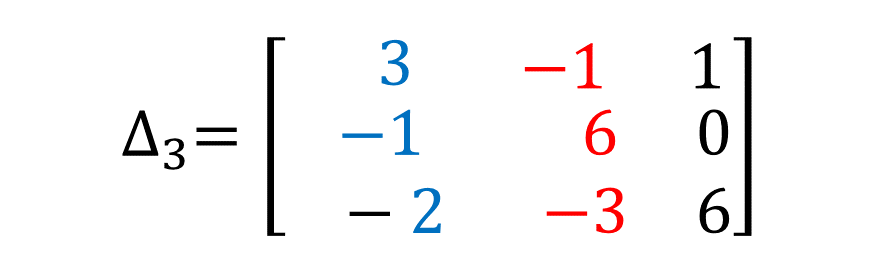
أخيرًا ، ابحث عن آخر 3 ∆. ما عليك سوى استبدال العمود الثالث بـ "عمود الإجابة" ، أي استبدل "Green guys في العمود الثالث بـ"Black guys "كما هو موضح أدناه.. cramer rule for circuit analyzing and simplification
∆3= + 3( 6x 6) – (- 3x 0) – [- 1(- 1x 6) – (- 2x 0)] + [1(- 1) x (- 3) – (- 2) x ( 6)]
∆3= 108 + 6 + 15
∆3= 117

الآن ، قم بحل وإيجاد القيم المجهولة للتيار ، أي { i 2, i 1 و i 3 }.

كما تقول قاعدة كرامر أن المتغيرات ، أي


i 1 = ∆1/∆ , i 2 = ∆2/∆ و i 3 = ∆3/∆

وبالتالي,

i 1 = ∆1/∆
= 117/39
i 1= 3A
i 2 و :
i 2 = = ∆2/∆
= 78/39
i 2 = 2A
i 3 وأخيرا ;
i 3 = ∆3/∆
= 117/39
i 3= 3A.

آمل أن تكون قد فهمت قاعدة كرامر جيدًا وأنك استمتعت بالبرنامج التعليمي خطوة بخطوة. من فضلك ، لا تنسى أن تشاركها مع أصدقائك. أدخل بريدك الإلكتروني في المربع أدناه للاشتراك. لذلك ، سوف نرسل لك المزيد من البرامج التعليمية مثل تلك المذكورة أعلاه. شكرا.

الوظائف ذات الصلة وأدوات تحليل الدوائر:

الصفحة الرئيسية
موسوعة المهندس الكهربائي
عرض المزيد
صفحة